Cone crusher dynamic cone and the eccentric sleeve centroid, not in its rotation center line, so during the operation of the cone crusher, as it inevitably produce inertial force and moment of inertia of the fixed points. This will rack bush and produces a spherical bushings with eccentric sleeve rotation and periodically changing force, causing harmful impact crusher vibration, and even affect the normal operation of the cone crusher. We must find the magnitude and direction of inertia force and moment of inertia to be balanced in order to eliminate or mitigate such harmful effects. This is the dynamic calculations.

According kinematics seen, crushers do regular exercise, also known as the cyclic movement. Fixed point O of external torque in order to move the cone as regular exercise, it is necessary to give a dynamic cone with a certain magnitude and direction, at the same time, the dynamic cone will inevitably produce an external bureau size equal and opposite moment of inertia . Moment of inertia of the moving cone demand in two ways: one is based on a dynamic cone implicated particle acceleration, relative acceleration and Coriolis acceleration, obtained by inertia force and moment of inertia. But according to the dynamic cone particle momentum, moment of momentum seek external moment - the moment of inertia. The results obtained by these two methods are the same, i.e., the inertia moment Ms as follows:

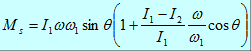
Where I1 is the moment of inertia of the moving cone axis itself, I2 is a dynamic cone and inertia on the axis perpendicular to itself through a fixed point O, w is the angular velocity of the eccentric sleeve implicated, θ is the dynamic cone crusher centerline axis folder obtuse, w1 is moving cone relative rotation angular velocity.

Dynamic cone crusher around the center line during rotation angular velocity w, based on mass motion theorem, dynamic cone inertial force:

Where r0 is the precession angle, ρ is the density of the moving cone and eccentric shaft material (t / m3), Z1, Z2 is moving cone hanging point to the distance (m) unit body, R1, R2 is fixed to the axis of the cone from the corresponding edge of the unit body (m).

Entire dynamic cone fixed point O of the total moment of inertia equal to external torque, namely Fc0.h = Ms, thus inertial forces can be obtained by moving cone force action line to a fixed point O distance h.

Eccentric sleeve member inertia force Fp (N) as: Fp = Gp.wr / g, where Gp is the mass of the eccentric sleeve member, w is the angular velocity of the eccentric sleeve, g is the gravitational acceleration, r is the eccentric sleeve parts Center Road from the machine centerline.

Since the eccentric sleeve member is rotatable about the center line machine, the force of inertia point on its center of gravity. Therefore, we need to calculate the center of gravity position eccentric sleeve member:

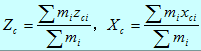
Meaning of the parameters in the formula: the machine to the center line and the eccentric sleeve surface prevail coordinate system is established. Zci the surface of the i-th coordinate focus away from the hollow cylinder, Xci is the first i coordinates of the center of gravity of each of the hollow cylinder from the centerline of the machine.

Eccentric sleeve member of the suspension points for the moment Mp: Mp = Fp × Lp, where Lp is the eccentric sleeve member suspended from the center of gravity to the point.